One-Sided Communication

This chapter describes performance issues related to MPI-2 standard one-sided communication:

• Introducing One-Sided Communication
• Comparing Two-Sided and One-Sided Communication
• Basic Sun MPI Performance Advice
• Case Study: Matrix Transposition

---

Introducing One-Sided Communication

The most common use of MPI calls is for two-sided communication. That is, if data moves from one process address space to another, the data movement has to be specified on both sides: the sender's and the receiver's. For example, on the sender's side, it is common to use MPI_Send() or MPI_Isend() calls. On the receiver's side, it is common to use MPI_Recv() or MPI_Irecv() calls. An MPI_Sendrecv() call specifies both a send and a receive.

Even collective calls, such as MPI_Bcast(), MPI_Reduce(), and MPI_Alltoall(), require that every process that contributes or receives data must explicitly do so with the correct MPI call.

The MPI-2 standard introduces one-sided communication. Notably, MPI_Put() and MPI_Get() allow a process to access another process address space without any explicit participation in that communication operation by the remote process.

---

Comparing Two-Sided and One-Sided Communication

In selected circumstances, one-sided communication offers several advantages:

• They can reduce synchronization and so improve performance. Note that two-sided communication implies some degree of synchronization. For example, a receive operation cannot complete before the corresponding send has started.

Further, because a sender cannot usually write directly into a receiver's address space, some intermediate buffer is likely to be used. If such buffering is small compared to the data volume, additional synchronization occurs whenever the sender must wait for the receiver to free up buffering. With one-sided communication, you must still specify synchronization to order memory operations, but you can amortize a single synchronization over many data movements.

• They can reduce data movement. As noted, two-sided communication sometimes introduces extra intermediate buffering, incurring extra data movement. An example of this would be an MPI program running on a large, shared-memory server. Interprocess communication usually depends upon having senders write to a shared-memory area and having receivers read from that area. This action requires twice as much data movement compared to the case where processes write directly to one another's address spaces. That extra data movement can affect aggregate backplane bandwidth, a critical resource in larger shared-memory servers.
• They can simplify programming. Note that information about a data transfer must be known and specified on only one side of the transfer, instead of two. This information is especially useful for dynamic, unstructured computations, where the traffic patterns change over the course of the computation.

---

Basic Sun MPI Performance Advice

Observe two principles to get good performance with one-sided communication with Sun MPI:

1. When creating a window (choosing what memory to make available for one-sided operations), use memory that has been allocated with the MPI_Alloc_mem routine. This suggestion in the MPI-2 standard benefits Sun MPI users:

http://www.mpi-forum.org/docs/mpi-20-html/node119.htm#Node119

2. Use one-sided communication over the shared memory (SHM) or remote shared memory (RSM) protocol module. That is, use one-sided communication between MPI ranks that either share the same shared-memory node or communicate via the Sun Fire Link interconnect. Protocol modules are chosen by Sun MPI at runtime and can be checked by setting the environment variable MPI_SHOW_INTERFACES=2 before launching your MPI job.

Further one-sided performance considerations for Sun MPI are discussed in Appendix A and Appendix B.

---

Case Study: Matrix Transposition

This section illustrates some of the advantages of one-sided communication with a particular example: matrix transposition. While one-sided communication is probably best suited for dynamic, unstructured computations, matrix transposition offers a relatively simple illustration.

Matrix transposition refers to the exchange of the axes of a rectangular array, flipping the array about the main diagonal. For example, in , after a transposition the array shown on the left side becomes the array shown on the right:

 FIGURE 5-1 Matrix Transposition

There are many ways of distributing elements of a matrix over the address spaces of multiple MPI processes. Perhaps the simplest is to distribute one axis in a block fashion. For example, our example transposition might appear distributed over two MPI processes (process 0 (p 0), and process 1 (p 1)) such as in :

 FIGURE 5-2 Matrix Transposition, Distributed Over Two Processes.

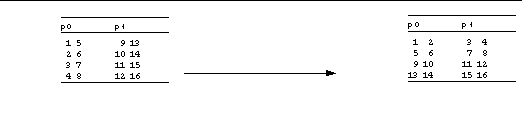
The ordering of multidimensional arrays within a linear address space varies from one programming language to another. A Fortran programmer, though, might think of the preceding matrix transposition as looking like :

 FIGURE 5-3 Matrix Transposition, Distributed Over Two Processes (Fortran Perspective).

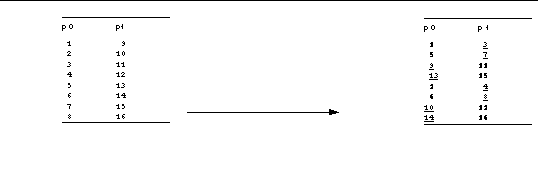
In the final matrix, as shown in , elements that have stayed on the same process show up in bold font, while elements that have moved between processes are underlined.

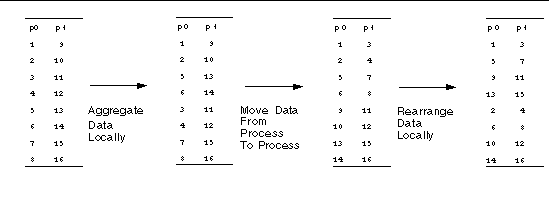
These transpositions move data between MPI processes. Note that no two matrix elements that start out contiguous end up contiguous. There are several strategies to effecting the interprocess data movement:

• Move one matrix element at a time. This strategy tends to introduce a lot of overhead and, therefore, performance penalties.
• Aggregate data locally within each MPI process, then move big blocks of matrix elements between processes, and finally rearrange data locally within each MPI process afterwards. This method makes the interprocess data movement relatively efficient, but entails a great deal of local data movement before and after the interprocess step.
• Move intermediate-size blocks of data between processes and do a moderate amount of local data rearrangement. This in-between approach is possible because there is some contiguity among data elements that travel between common MPI processes.

is an example of maximal aggregation for our 4x4 transposition:

 FIGURE 5-4 Matrix Transposition, Maximal Aggregation for 4X4 Transposition

Test Program A

Program A, shown in CODE EXAMPLE 5-1:

• Aggregates data locally.
• Establishes interprocess communication using a two-sided collective call MPI_Alltoall().
• Rearranges data locally using the call DTRANS(), the optimized transpose in the Sun Performance Library.

CODE EXAMPLE 5-1 Test Program A

include "mpif.h"   real(8), allocatable, dimension(:) :: a, b, c, d real(8) t0, t1, t2, t3   ! initialize parameters call init(me,np,n,nb)   ! allocate matrices allocate(a(nb*np*nb)) allocate(b(nb*nb*np)) allocate(c(nb*nb*np)) allocate(d(nb*np*nb))   ! initialize matrix call initialize_matrix(me,np,nb,a)   ! timing do itime = 1, 10 call MPI_Barrier(MPI_COMM_WORLD,ier) t0 = MPI_Wtime()   ! first local transpose do k = 1, nb do j = 0, np - 1 ioffa = nb * ( j + np * (k-1) ) ioffb = nb * ( (k-1) + nb * j ) do i = 1, nb b(i+ioffb) = a(i+ioffa) enddo enddo enddo   t1 = MPI_Wtime()   ! global all-to-all call MPI_Alltoall(b, nb*nb, MPI_REAL8, & c, nb*nb, MPI_REAL8, MPI_COMM_WORLD, ier) t2 = MPI_Wtime()   ! second local transpose call dtrans(`o', 1.d0, c, nb, nb*np, d) call MPI_Barrier(MPI_COMM_WORLD,ier) t3 = MPI_Wtime()   if ( me .eq. 0 ) & write(6,'(f8.3," seconds; breakdown on proc 0 = ",3f10.3)') & t3 - t0, t1 - t0, t2 - t1, t3 - t2 enddo   ! check call check_matrix(me,np,nb,d) deallocate(a) deallocate(b) deallocate(c) deallocate(d)   call MPI_Finalize(ier) end

Test Program B

Program B, shown in CODE EXAMPLE 5-2:

• Aggregates data locally.
• Establishes interprocess communication using a series of one-sided MPI_Put() calls.
• Rearranges data locally using a DTRANS() call.

Test program B should outperform test program A because one-sided interprocess communication can write more directly to a remote process address space.