| C H A P T E R 6 |
|
Sun S3L Performance Guidelines |
This chapter discusses a variety of performance issues as they relate to use of Sun S3L routines. The discussions are organized along the following lines:
Sun S3L relies on functions in the Sun Performance Library (libsunperf) software for numerous computations within each process. For best performance, make certain your executable uses the architecture-specific version of the libsunperf library. You can do this by linking your program using the -xarch=v8plusa option for 32-bit executables or the -xarch=v9a option for 64-bit executables.
At runtime, the environment variable LD_LIBRARY_PATH can be used to override link-time library choices. Ordinarily, you should not use this environment variable, as it might link suboptimal libraries, such as the generic SPARC version, rather than one optimized for an UltraSPARC processor.
To unset the LD_LIBRARY_PATH environment variable, use
% unsetenv LD_LIBRARY_PATH |
To confirm which libraries will be linked at runtime, use
% ldd executable |
If Sun S3L detects that a suboptimal version of the libsunperf library was linked in, it will print a warning message. For example:
S3L warning: Using libsunperf not optimized for UntraSPARC. For better performance, link using -xarch=v8plusa |
Many Sun S3L functions support ScaLAPACK application programming interfaces (APIs). This means you can increase the performance of many parallel programs that use ScaLAPACK calls simply by linking in Sun S3L instead of the public domain software.
Alternatively, you might convert ScaLAPACK array descriptors to Sun S3L array handles and call Sun S3L routines explicitly. By converting the ScaLAPACK array descriptors to the equivalent Sun S3L array handles, you can visualize distributed ScaLAPACK arrays by using Prism and use the Sun S3L simplified array syntax for programming. You will also have full use of the Sun S3L toolkit functions.
Sun S3L provides the function S3L_from_ScaLAPACK_desc that performs this API conversion for you. Refer to the S3L_from_ScaLAPACK_desc man page for details.
One of the most significant performance-related factors in Sun S3L programming is the distribution of Sun S3L arrays among MPI processes. Sun S3L arrays are distributed, axis by axis, using mapping schemes that are familiar to users of ScaLAPACK or High Performance Fortran. That is, elements along an axis might have any one of the following mappings:
FIGURE 6-1 illustrates these mappings with examples of a one-dimensional array distributed over four processes.
For multidimensional arrays, mapping is specified separately for each axis, as shown in FIGURE 6-2. This diagram illustrates a two-dimensional array's row and column axes being distributed among four processes. Four examples are shown, using a different combination of the three mapping schemes in each. The value represented in each array element is the rank of the process on which that element resides.


In certain respects, local distribution is simply a special case of block distribution, which is just a special case of cyclic distribution. Although related, the three distribution methods can have very different effects on both interprocess communication and load balancing among processes. TABLE 6-1 summarizes the relative effects of the three distribution schemes on these performance components.
|
Load balancing (such as operations on left-half of data set) |
The next two sections provide guidelines for when you should use local and cyclic mapping. When none of the conditions described next apply, use block mapping.
The chief reason to use local mapping is that it eliminates certain communication.
The following are two general classes of situations in which local distribution should be used:
Some algorithms in linear algebra operate on portions of an array that diminish as the computation progresses. Examples within Sun S3L include logical unit (LU) decomposition (S3L_lu_factor and S3L_lu_solve routines), singular value decomposition (S3L_gen_svd routine), and the least-squares solver (S3L_gen_lsq routine). For these Sun S3L routines, cyclic distribution of the data axes improves load balancing.
When declaring an array, you must specify the size of the block to be used in distributing the array axes. Your choice of block size not only affects load balancing, it also trades off between concurrency and cache use efficiency.
Specifying large block sizes will block multiple computations together. This process leads to various optimizations, such as improved cache reuse and lower MPI latency costs. However, blocking computations reduces concurrency, which inhibits parallelization.
A block size of 1 maximizes concurrency and provides the best load balancing. However, small block sizes degrade cache use efficiency.
Because the goals of maximizing concurrency and cache use efficiency conflict, you must choose a block size that will produce an optimal balance between them. The following guidelines are intended to help you avoid extreme performance penalties:
There is no simple formula for determining an optimal block size that will cover all combinations of matrices, algorithms, numbers of processes, and other such variables. The best guide is experimentation, while keeping the points just outlined in mind.
This section demonstrates the load balancing benefits of cyclic distribution for an algorithm that sums the lower triangle of an array.
It begins by showing how block distribution results in a load imbalance for this algorithm (see FIGURE 6-3). In this example, the array's column axis is block-distributed across processes 0-3. Because process 0 must operate on many more elements than the other processes, total computational time will be bounded by the time it takes process 0 complete. The other processes, particularly process 3, will be idle for much of that time.

FIGURE 6-4 shows how cyclic distribution of the column axis delivers better load balancing. In this case, the axis is distributed cyclically, using a block size of 1. Although process 0 still has more elements to operate on than the other processes, cyclical distribution significantly reduces its share of the array elements.

The improvement in load balancing is summarized in TABLE 6-2. In particular, note the decrease in the number of elements allocated to process 0, from 54 to 36. Because process 0 still determines the overall computational time, this drop in element count can be seen as a computational speed-up of 150 percent.
Ordinarily, Sun S3L will map an S3L array onto a process grid whose logical organization is optimal for the operation to be performed. You can assume that, with few exceptions, performance will be best on the default process grid.
However, if you have a clear understanding of how a Sun S3L routine will make use of an array and you want to try to improve the routine's performance beyond that provided by the default process grid, you can explicitly create process grids usingthe S3L_set_process_grid toolkit function. This toolkit function allows you to control the following process grid characteristics.
For some Sun S3L routines, a process grid's layout can affect both load balancing and the amount of interprocess communication that a given application experiences. For example:
Note that, these generalizations can, in some situations, be nullified by various other parameters that also affect performance. If you choose to create a nondefault process grid, you are most likely to arrive at an optimal block size through experimentation, using the guidelines described here as a starting point.
The runtime mapping of a process grid to nodes in a cluster can also influence the performance of Sun S3L routines. Communication within a multidimensional process grid generally occurs along a column axis or along a row axis. Thus, you should map all the processes in a process grid column (or row) onto the same node so that the majority of the communication takes place within the node.
Runtime mapping of process grids is effected in two parts:
The two mapping stages are illustrated in FIGURE 6-6.
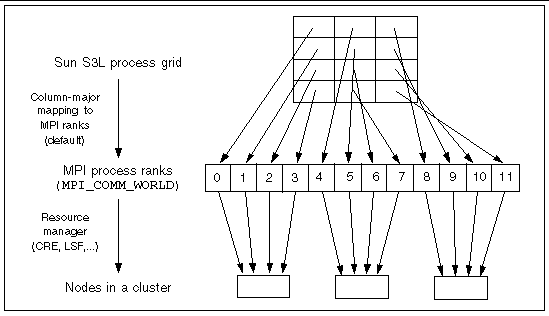
Neither stage of the mapping, by itself, controls performance. Rather, it is the combination of the two that determines the extent to which communication within the process grid will stay on a node or will be carried out over a network connection, which is an inherently slower path.
Although the ability to control process grid layout and the mapping of process grids to nodes give the programmer considerable flexibility, it is generally sufficient for good performance to:
For example, assume that 12 MPI processes are organized as a 4x3, column-major process grid. To ensure that communication between processes in the same column remain on node, the first four processes must be mapped to one node, the next four processes to one node (possibly the same node as the first four processes), and so forth.
If your runtime manager is CRE, use:
% mprun -np 12 -Z 4 a.out |
% bsub -I -n 12 -R "span[ptile=4]" a.out |
Note that the semantics of the CRE and LSF examples differ slightly. Although both sets of command-line arguments result in all communication within a column being on-node, they differ in the following way:
Chapter 8 contains a fuller discussion of runtime mapping.
Yet another way of reducing communication costs is to run on a single SMP node and allocate Sun S3L data arrays in shared memory. This method allows some Sun S3L routines to operate on data in place. Such memory allocation must be performed with the S3L_declare or S3L_declare_detailed routine.
When declaring an array that will reside in shared memory, you need to specify how the array will be allocated. Specify the method of allocation with the atype argument. TABLE 6-3 lists the two atype values that are valid for declaring an array for shared memory and the underlying mechanism that is used for each.
Smaller data types have higher ratios of floating-point operations to memory traffic, and so generally provide better performance. For example, 4-byte floating-point elements are likely to perform better than double-precision 8-byte elements. Similarly, single-precision complex will generally perform better than double-precision complex.
This section contains performance-related information about individual Sun S3L routines. TABLE 6-4 summarizes some recommendations.
Symbols used in TABLE 6-4 are defined in FIGURE 6-7:

The operation count expressions shown in TABLE 6-4 provide a yardstick by which a given routine's performance can be evaluated. They can also be used to predict how runtimes are likely to scale with problem size.
For example, assume a matrix multiply yields 350 MFLOPS on a 250-MHz UltraSPARC processor, which has a peak performance of 500 MFLOPS. The floating-point efficiency is then 70 percent, which can be evaluated for acceptability.
Floating-point efficiency is only an approximate guideline for determining an operation's level of performance. It cannot exceed 100 percent, but it might legitimately be much lower under various conditions, such as when operations require extensive memory references or when there is an imbalance between floating-point multiplies and adds. Often, bandwidth to local memory is the limiting factor. For iterative algorithms, the operation count is not fixed.
The S3L_mat_mult routine computes the product of two matrices. It is most efficient when:
If it is not possible to provide these conditions for a matrix multiply, ensure that the corresponding axes of the two factors are distributed consistently. For example, for a matrix multiply of size (m,n) = (m,k) x (k,n), use the same block size for the second axis of the first factor and the first axis of the second factor (represented by k in each in case).
Sun S3L employs its own heuristics for distributing sparse matrices over MPI processes. Consequently, you do not need to consider array distribution or process grid layout for the S3L_matvec_sparse routine.
Shared-memory optimizations are performed only when the sparse matrix is in the S3L_SPARSE_CSR format and the input and output vectors are both allocated in shared memory.
The S3L_lu_factor routine uses a parallel, block-partitioned algorithm derived from the ScaLAPACK implementation. It provides best performance for arrays with cyclic distribution.
The following are useful guidelines to keep in mind when choosing block sizes for the S3L_lu_factor routine:
The S3L_lu_factor routine has special optimizations for double-precision, floating-point matrices. Based on knowledge of the external cache size and other process parameters, it uses a specialized matrix multiply routine to increase overall performance, particularly on large matrices.
These optimizations are available to arrays that meet the following conditions:
When deciding on a process grid layout for LU factorization, your choices will involve making a trade-off between load balancing and minimizing communication costs. Pivoting will usually be responsible for most communication. The extreme ends of the trade-off spectrum follow:
Some experimentation will be necessary to arrive at the optimal trade-off for your particular requirements.
Performance is best when the extents of the array can be factored into small, prime factors no larger than 13.
The operation count expressions given in TABLE 6-4 for the FFT family of routines provide a good approximation. However, the actual count will depend to some extent on the radix (factors) used. In particular, for a given problem size, the real-to-complex and complex-to-real FFTs have half the operation counts and half the memory requirements of their complex-to-complex counterparts.
The transformed axis should be local. If a multidimensional transform is desired, make all but the last axis local.
It is likely that the resulting transpose will dominate the computation, at least in a multinode cluster. See The S3L_trans Routine.
These routines tend to have relatively low communication costs, and so tend to scale well.
For best performance of the factorization routines, have all the axes of the array factored locally, except for the last axis, which should be block distributed.
Conversely, the corresponding solver routines perform best when the first axis of the right side array is block distributed and all other axes are local.
Performance of the S3L_sym_eigen routine is sensitive to interprocess latency.
If both eigenvectors and eigenvalues are computed, execution time might be as much as an order of magnitude longer than if only eigenvalues are computed.
The S3L_rand_fib and S3L_rand_lcg routines initialize parallel arrays using a Lagged-Fibonacci and a Linear Congruential random number generator, respectively. An array initialized by the Lagged-Fibonacci routine will vary depending on the array distribution. In contrast, array initialization by the Linear Congruential method will produce the same result, regardless of the array's distribution.
Because the Linear Congruential random number generator must ensure that the resulting random numbers do not depend on how the array is distributed, it has the additional task of keeping account of the global indices of the array elements. This extra overhead is minimized when local or block distribution is used and greatly increased by distributing the array cyclically. The S3L_rand_lcg routine can be two to three times slower with cyclic distributions than with local or block distributions.
Because the S3L_rand_fib routine fills array elements with random numbers regardless of the elements' global indices, it is significantly faster than with the S3L_rand_lcg routine.
The S3L_rand_lcg routine is based on 64-bit strings. This means it performs better on S3L_long_integer data types than on S3L_integer elements.
The S3L_rand_fib routine, on the other hand, is based on 32-bit integers. It generates S3L_integer elements twice as fast as for S3L_long_integer output.
Both algorithms generate floating-point output more slowly than integers, since they must convert random bit strings into floating-point output. Complex numbers are generated at half the rate of real numbers, since twice as many must be generated.
S3L_gen_lsq finds the least squares solution of an overdetermined system. It is implemented with a QR algorithm. The operation count, shown in TABLE 6-4, applies to real, square matrices. For a real, rectangular (M,N) matrix, the operation count scales as:
For complex elements, the operation count is four times as great.
For S3L_gen_svd, the convergence of the iterative algorithm depends on the matrix data. Consequently, the count is not well-defined for this routine. However, the S3L_gen_svd routine does tend to scale as N3.
If the singular vectors are computed, the runtime can be roughly an order of magnitude longer than if only singular values are extracted.
The A, U, and V arrays should all be on the same process grid for best performance.
Most of the time spent in this routine is in the S3L_mat_vec_sparse routine.
Overall performance depends on more than just the floating-point rate of that subroutine. It is also significantly influenced by the matrix data and by the choice of solver, preconditioner, initial guess, and convergence criteria.
The performance of these functions depends on the performance of Sun S3L FFTs and, consequently, on the performance of the Sun S3L transposes.
These routines do not involve floating-point operations. The operation count can vary greatly, depending on the distribution of keys, but it will typically scale from O(N) to O(N log(N)).
Sorts of 64-bit integers can be slower than sorts of 64-bit floating-point numbers.
The S3L_trans routine provides communication support to the Sun FFTs as well as to many other Sun S3L algorithms. Best performance is achieved when axis extents are all multiples of the number of processes.
The Sun S3L Toolkit functions are primarily intended for convenience rather than performance. However, some significant performance variations do occur. For example:
Copyright © 2003, Sun Microsystems, Inc. All rights reserved.