| Oracle Data Mining Concepts 10g Release 1 (10.1) Part Number B10698-01 |
|
|
View PDF |
| Oracle Data Mining Concepts 10g Release 1 (10.1) Part Number B10698-01 |
|
|
View PDF |
Data mining tasks in the ODM PL/SQL interface include model building, model testing and computing lift for a model, and model applying (scoring).
The development methodology for data mining using DBMS_DATA_MINING has two phases:
After you've analyzed the problem and data, use the DBMS_DATA_MINING and DBMS_DATA_MINING_TRANSFORM packages to develop a PL/SQL application that performs the data mining:
Note that the build, test, and score data sets must be prepared in an identical manner for mining results to be meaningful.
The DBMS_DATA_MINING package creates a mining model for a mining function using a specified mining algorithm that supports the function. The algorithm can be influenced using specific algorithm settings. Model build is synchronous in the PL/SQL interface. After a model is built, there is single-user, multi-session access to the model.
A model is identified by its name. Like tables in the database, a model has storage associated with it. The form, shape, and content of this storage is opaque to the user. However, the user can view the contents of a model -- that is, the patterns and rules that constitute a mining model -- using algorithm-specific GET_MODEL_DETAILS functions.
The DBMS_DATA_MINING package supports Classification, Regression, Association, Clustering, and Feature Extraction. You specify the mining function as a parameter to the BUILD procedure.
Each mining function can be implemented using one or more algorithms. Table 7-1 provides a list of supported algorithms. There is a default algorithm for each mining function, but you can override this default through an explicit setting in the settings table.
Each algorithm has one or more settings that influence the way it builds the model. There is a default set of algorithm settings for each mining algorithm. These defaults are provided through the transformation GET_DEFAULT_SETTINGS. To override the defaults, you must provide the choice of the algorithm and the settings for the algorithm through a settings table input to the BUILD Procedure.
The settings table is a simple relational table with a fixed schema. The name of the settings table can be whatever name you choose. The settings table must have exactly two columns with names and types as follows:
The values specified in a settings table override the default values. The values in the setting_name column are one or more of several constants defined in the DBMS_DATA_MINING package. The values in the setting_value column are either predefined constants or actual numerical value corresponding to the setting itself. The setting_value column is of type VARCHAR2; you must cast numerical inputs to string using the TO_CHAR() function before input into the settings table.
The following example shows how to create a settings table for an SVM classification model, and edit the individual values using SQL DML.
CREATE TABLE drugstore_settings (
setting_name VARCHAR2(30),
setting_value VARCHAR2(128));
-- override the default for complexity factor for SVM Classification
INSERT INTO drugstore_model_settings (setting_name, setting_value)
VALUES (dbms_data_mining.svms_complexity_fator, TO_CHAR(0.081));
COMMIT;
The transformation DATA_MINING_GET_DEFAULT_SETTINGS contains all the default settings for mining functions and algorithms. If you intend to override all the default settings, you can create a seed settings table and edit them using appropriate DML.
CREATE TABLE drug_store_settings AS
SELECT setting_name, setting_value
FROM DM_DEFAULT_SETTINGS
WHERE setting_name LIKE 'SVMS_%';
-- update the values using appropriate DML
You can also create a settings table based on another model's settings using GET_MODEL_SETTINGS, as shown in the example below.
CREATE TABLE my_new_model_settings AS
SELECT setting_name, setting_value
FROM DBMS_DATA_MINING.GET_MODEL_SETTINGS('my_other_model');
Priors or Prior Probabilities are discussed in Section 3.1.2 You can specify the priors in a prior probabilities table as an optional function setting when building classification models.
The prior probabilities table has a fixed schema. For numerical targets, use the following schema:
For categorical targets, use the following schema:
Specify the name of the prior probabilities table as input to the setting_value column in the settings table, with the corresponding value for the setting_name column to be DBMS_DATA_MINING.clas_priors_table_name, as shown below:
INSERT INTO drugstore_settings (setting_name, setting_value) VALUES (DBMS_DATA_MINING.class_priors_table_name, 'census_priors');
COMMIT;
Costs are discussed in Section 3.1.1. You specify costs in a cost matrix table. The cost matrix table has a fixed schema. For numerical targets, use the following schema:
For categorical targets, use the following schema:
The DBMS_DATA_MINING package enables you to evaluate the cost of predictions from classification models in an iterative manner during the experimental phase of mining, and to eventually apply the optimal cost matrix to predictions on the actual scoring data in a production environment.
The data input to each COMPUTE procedure in the package is the result generated from applying the model on test data. If you provide a cost matrix as an input, the COMPUTE procedure generates test results taking the cost matrix into account. This enables you to experiment with various costs for a given prediction against the same APPLY results, without rebuilding the model and applying it against the same test data for every iteration.
Once you arrive at an optimal cost matrix, you can input this cost matrix to the RANK_APPLY procedure along with the results of APPLY on your scoring data. RANK_APPLY will provide your new data ranked by cost.
There are several sets of mining operations supported by the DBMS_DATA_MINING package:
The first set of operations are DDL-like operations. The last set consists of utilities. The remaining sets of operations are query-like operations in that they do not modify the model.
In addition to the operations, the following capabilities are also provided as part of the Oracle Data Mining installation:
Mining results are either returned as result sets or persisted as fixed schema tables.
The BUILD operation creates a mining model. The GET_MODEL_DETAILS functions for each supported algorithm permit you to view the model. In addition, GET_MODEL_SIGNATURE and GET_MODEL_SETTINGS provide descriptive information about the model.
APPLY creates and populates a fixed schema table with a given name. The schema of this table varies based on the particular mining function, algorithm, and target attribute type -- numerical or categorical.
RANK_APPLY takes an APPLY result table as input and generates another table with results ranked based on a top-N input, and for classification models, also based on cost. The schema of this table varies based on the particular mining function, algorithm, and the target attribute type -- numerical or categorical.
DBMS_DATA_MINING includes the following procedures for testing classification models:
These procedures are described in the DBMS_DATA_MINING chapter of PL/SQL Packages and Types Reference.
The rest of this section describes confusion matrix, lift, and receiver operating characteristics.
ODM supports the calculation of a confusion matrix to asses the accuracy of a classification model. A confusion matrix is a 2-dimensional square matrix. The row indexes of a confusion matrix correspond to actual values observed and used for model testing; the column indexes correspond to predicted values produced by applying the model to the test data. For any pair of actual/predicted indexes, the value indicates the number of records classified in that pairing. For example, a value of 25 for an actual value index of "buyer" and a predicted value index of "nonbuyer" indicates that the model incorrectly classified a "buyer" as a "nonbuyer" 25 times. A value of 516 for an actual/predicted value index of "buyer" indicates that the model correctly classified a "buyer" 516 times.
The predictions were correct 516 + 725 = 1241 times, and incorrect 25 + 10 = 35 times. The sum of the values in the matrix is equal to the number of scored records in the input data table. The number of scored records is the sum of correct and incorrect predictions, which is 1241 + 35 = 1276. The error rate is 35/1276 = 0.0274; the accuracy rate is 1241/1276 = 0.9725.
A confusion matrix provides a quick understanding of model accuracy and the types of errors the model makes when scoring records. It is the result of a test task for classification models.
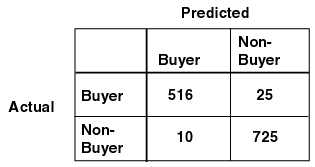
Text description of the illustration confmtrx.gif
ODM supports computing lift for a classification model. Lift can be computed for both binary (2 values) target fields and multiclass (more than 2 values) target fields. Given a designated positive target value (that is, the value of most interest for prediction, such as "buyer," or "has disease"), test cases are sorted according to how confidently they are predicted to be positive cases. Positive cases with highest confidence come first, followed by positive cases with lower confidence. Negative cases with lowest confidence come next, followed by negative cases with highest confidence. Based on that ordering, they are partitioned into quantiles, and the following statistics are calculated:
Cumulative targets can be computed from the quantities that are available in the LiftRresultElement using the following formula:
Another useful method for evaluating classification models is Receiver Operating Characteristics (ROC) analysis. ROC curves are similar to Lift charts in that they provide a means of comparison between individual models and determine thresholds which yield a high proportion of positive hits. Specifically, ROC curves aid users in selecting samples by minimizing error rates. ROC was originally used in signal detection theory to gauge the true hit versus false alarm ratio when sending signals over a noisy channel.
The horizontal axis of an ROC graph measures the false positive rate as a percentage. The vertical axis shows the true positive rate. The top left hand corner is the optimal location in an ROC curve, indicating high TP (true-positive) rate versus low FP (false-positive) rate. The ROC Area Under the Curve is useful as a quantitative measure for the overall performance of models over the entire evaluation data set. The larger this number is for a specific model, the better. However, if the user wants to use a subset of the scored data, the ROC curves help in determining which model will provide the best results at a specific threshold.
In the example graph in Figure 7-2, Model A clearly has a higher ROC Area Under the Curve for the entire data set. However, if the user decides that a false positive rate of 40% is the maximum acceptable, Model B is better suited, since it achieves a better error true positive rate at that false positive rate.
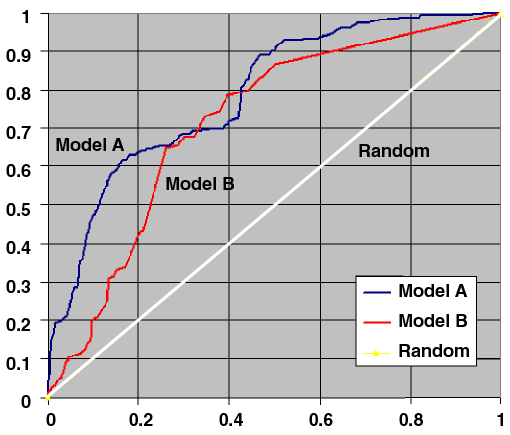
Text description of the illustration roc3.gif
Besides model selection the ROC also helps to determine a threshold value to achieve an acceptable trade-off between hit (true positives) rate and false alarm (false positives) rate. By selecting a point on the curve for a given model a given trade-off is achieved. This threshold can then be used as a post-processing for achieving the desired performance with respect to the error rates. ODM models by default use a threshold of 0.5. This is the confusion matrix reported by the test in the ODM Java interface.
The Oracle Data Mining ROC computation calculates the following statistics:
The most commonly used metrics for regression models are root mean square error and mean absolute error. You can use SQL queries described in Oracle Data Mining Application Developer's Guide to compute those metrics.
The regression test results provide measures of model accuracy: root mean square error and mean absolute error of the prediction.
The following query calculates root mean square.
SELECT sqrt(avg((A.prediction - B.target_column_name) *
(A.prediction - B.target_column_name))) rmse
FROMapply_results_table A, targets_table B
WHERE A.case_id_column_name = B.case_id_column_name;
Given the targets table generated from the test data with the schema:
and apply results table for regression with the schema:
and a (optional) normalization table with the schema:
the query for mean absolute error is:
SELECT /*+PARALLEL(T) PARALLEL(A)*/
AVG(ABS(T.actual_value - T.target_value)) mean_absolute_error
FROM (SELECT B.case_id_column_name,
(B.target_column_name * N.scale + N.shift) actual_value
FROM targets_table B,
normalization_table N
WHERE N.attribute_name = B.target_column_name AND
B.target_column_name = 1) T, apply_results_table_name A
WHERE A.case_id_column_name = T.case_id_column_name;
You can fill in the italicized values with the actual column and table names chosen by you. If the data is not normalized, you can eliminate those references from the subquery.
Oracle supports data mining model export and import between Oracle databases or schemas to provide a way to move models. DBMS_DATA_MINING does not support model export and import via PMML.
Model export/import is supported at different levels, as follows:
expdp utility, all the existing data mining models in the database will be exported. When a DBA imports a database dump using the impdp utility, all the data mining models in the dump will be restored.expdp, all the data mining models in the schema will be exported. When the user or DBA imports the schema dump using impdp, all the models in the dump will be imported.DBMS_DATA_MINING.export_model() and import specified models using DBMS_DATA_MINING.import_model().DBMS_DATA_MINING supports export and import of models based on the Oracle DBMS Data Pump. Where you export a model, the tables that constitute the model and the associated metadata are written to a dump file set that consists of one or more files. When you import a model, the tables and metadata are retrieved from the file and restored in the new database.
For information about requirements for the application system, see Chapter 9.
For detailed information about the export/import transformation, see the Oracle Data Mining Application Developer's Guide.