4 - C H A P T E R -

C H A P T E R 4

Multiple Instance

Most Sun S3L routines support multiple instances. That is, they enable you to perform multiple independent operations on different data sets concurrently. The multiple instance discussions in this chapter are organized into the following sections:

Defining Multiple Independent Data Sets

Rules for Data Axes and Instance Axes

Specifying Single-Instance vs. Multiple-Instance Operations

Defining Multiple Independent Data Sets

To perform a Sun S3L operation on multiple independent data sets in parallel, you must embed the multiple independent instances of each operand or result argument in a parallel array.

The shape of the parallel array is defined by two kinds of axes:

Data axes define the geometry of the individual instances of the operand or result.

Instance axes label the multiple instances.

FIGURE 4-1 illustrates this with an example of a matrix-vector multiplication operation in which four independent products are computed simultaneously. It shows how the destination and source vectors and the source matrix are organized with respect to the data and instance axes:

The four destination vectors are embedded in a 2D parallel array with one data axis and one instance axis.

The four source vectors are similarly embedded in another parallel array.

The source matrices are embedded in a 3D parallel array.

The instances within each variable are labeled 0 through 3.

FIGURE 4-1 A Multiple-Instance Matrix-Vector Multiplication Problem

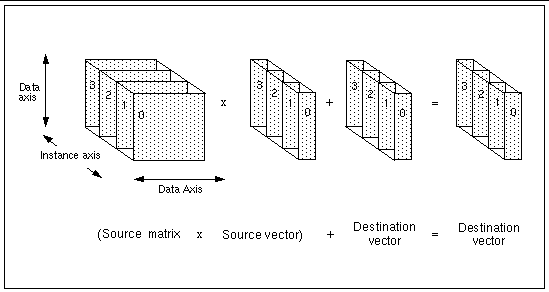
Graphic image illustrating a multiple-instance matrix-vector multiplication problem.

The logical unit on which the routine operates--sometimes called a cell--is defined by the data axes. The instance axes define the geometry of the frame in which the cells are embedded. The 3D parallel array shown in FIGURE 4-1 is a frame containing four 2-dimensional cells.

The product of the lengths of the instance axes is the total number of instances. The product of the lengths of the data axes is the size of the cell.

Rules for Data Axes and Instance Axes

When you organize your data to form cells and frames for a multiple-instance operation, apply the following rules:

All parallel arrays involved in the operation must have the same number of instance axes.

Counting up through the instance axes of the parallel arrays (excluding the data axes), corresponding instance axes must occur in the same order in each operand or result.

The corresponding instance axes of the operands or results must have identical lengths. Certain routines also require that corresponding instance axes must also have identical layouts. The situations where identical layouts are required are identified in the applicable man pages.

The lengths of the data axes must be defined so that the operation makes sense. For example, in matrix multiplication, the data axis lengths of the operand and result matrices must obey the standard rules for axis lengths in matrix multiplication. Specific requirements for data axis lengths are provided in the applicable man pages.

Except where explicitly noted, Sun S3L supports all combinations of layouts for data axes and instance axes. Which layout will provide the best performance for any given operation depends largely on the nature of the operation.

In most cases, however, performance is best when the cells (that is, all of the data axes) are local to a processing element. Instance axes are typically defined as nonlocal axes. Some man pages for Sun S3L routines contain specific information about optimizing layouts.

Specifying Single-Instance vs. Multiple-Instance Operations illustrates these rules being applied in a matrix-vector multiplication example.

Note - Most Sun S3L routines impose few or no restrictions on where the instance axes can occur in a parallel array.

Specifying Single-Instance vs. Multiple-Instance Operations

Sun S3L routines that support multiple instances have the same calling sequence for single-instance and multiple-instance operations. The methods for specifying single-instance and multiple-instance operations depend on which routine you are calling. The man pages for routines that are capable of multiple-instance operation contain specific information for their respective routines.

Example 1: Matrix-Vector Multiplication explains the differences between single- and multiple-instance operation for the matrix-vector-multiplication routine.

Example 2: Fast Fourier Transforms discusses use of multiple instances in FFTs.

Example 1: Matrix-Vector Multiplication

When you call the matrix-vector-multiplication routine, S3L_mat_vec_mult, the dimensionality of the arguments you supply determines whether the routine performs a single-instance or multiple-instance operation. The F77 form of this Sun S3L function is:

S3L_mat_vec_mult(y, a, x, y_vector_axis, row_axis, col_axis,

x_vector_axis, ier)

Note - The S3L_mat_vec_mult routine requires you to specify which axes you are using as data axes for each matrix or vector argument.

Single-Instance Operation

To perform a single-instance operation, specify each vector argument as a 1D parallel array and each matrix argument as a 2D parallel array. (Alternatively, you can declare these arguments to have more dimensions, but all instance axes must have length 1.)

For example, a single-instance operation in F77 can be performed by first defining the block-distributed arrays:

 integer*8 a, x, y

 integer*4 ext(2), axis_is_local(2)

 integer*4 ier

 axis_is_local(1) = 0

 axis_is_local(2) = 0

 ext(1) = p

 ext(2) = q

 call s3l_declare(a, 2, ext, S3L_float, axis_is_local,

$    S3L_USE_MALLOC, ier)

 call s3l_declare(x, 1, ext, S3L_float, axis_is_local,

$    S3L_USE_MALLOC, ier)

 call s3l_declare(y, 1, ext, S3L_float, axis_is_local,

$    S3L_USE_MALLOC, ier)

and then using

call S3L_mat_vec_mult(y, a, x, 1, 1, 2, 1, ier)

Arrays x and y are 1D. The definitions of x_vector_axis = 1 and col_axis = 2 indicate that the product a(i, j) * x(j) will be evaluated for all values of j. These products will be summed over the first index of a (row_axis = 1), and the result added to the corresponding element in y. The equivalent code is

do i = 1, p

    sum = 0.0

    do j = i, q

        sum = sum + a(i, j) * x(j)

    enddo

enddo

Multiple-Instance Operation

To perform a multiple-instance operation, embed the multiple instances of each vector argument in a parallel array of rank greater than 1, and embed the multiple instances of each matrix argument in a parallel array of rank greater than 2.

For example, the simplest multiple-instance matrix-vector multiplication involves the definition of one instance axis.

 integer*8 a, x, y

 integer*4 ext(3), axis_is_local(3)

 integer*4 ier

 axis_is_local(1) = 0

 axis_is_local(2) = 0

 axis_is_local(3) = 0

 ext(1) = p

 ext(2) = q

 ext(3) = r

 call s3l_declare(a, 3, ext, S3L_float, axis_is_local,

$    S3L_USE_MALLOC, ier)

 ext(1) = q

 ext(2) = r

 call s3l_declare(x, 2, ext, S3L_float, axis_is_local,

$    S3L_USE_MALLOC, ier)

 ext(1) = p

 ext(2) = r

 call s3l_declare(y, 2, ext, S3L_float, axis_is_local,

$    S3L_USE_MALLOC, ier)

In this code, all three arrays contain an instance axis of length r. In addition, each instance axis is the rightmost axis in the array declaration. In other words, the order of data axes and instance axes is the same in all three arrays. These axis definitions produce arrays whose geometries are outlined in FIGURE 4-1. In the illustration, r = 4.

Multiplication using these arrays is then performed by:

call S3L_mat_vec_mult(y, a, x, 1, 1, 2, 1, ier)

In analyzing the operations performed in this call, it is useful to define s0, the index along the instance axis. For a given value of s0, the following operations will be done:

The product a(i, j, s0) * x(j, s0) will be calculated for all j. This is indicated by the values of the arguments x_vector_axis and col_axis, which are 1 and 2 respectively.

The above product will be summed over i, the first index of a (row_axis = 1), and the result added to y(i, s0).

These two operations will be performed for all 1 <= s0 <= r. In other words, the matrix-vector multiplication will be evaluated for all instances:

y(:, s0) * a(:, :, s0) * x(:, s0)

The order in which these instances are evaluated depends on the layouts of the arrays. Since all arrays are block-distributed along all axes, it is possible for one set of processes to work on the first instance:

y(:, 1) = a(:, :, 1) * x(:, 1)

while another set of processes evaluates the N-th instance at the same time--that is, in parallel:

y(:, N) = a(:, :, N) * x(:, N)

The Importance of Data Layout

The extent of parallelism depends on the details of the data layouts, particularly on the mapping of the data and instance axes to the underlying process grid axes. The highest degree of parallelism is achieved when all data axes are local and all instance axes are distributed.

The use of local data axes forces each cell (that is, all data axes) to reside entirely in just one process. The use of distributed instance axes spreads the collection of cells over the process grid, resulting in better load-balancing among processes.

Multiple-instance operations are usually most efficient when each cell (all of the data axes) resides on one process. Local distribution of data axes is illustrated below, using a Sun S3L array of rank 5, with the first two axes being the data axes and the other three being instance axes.

 integer*8 a, x, y

 integer*4 mat_ext(5), mat_axis_is_local(5)

 integer*4 vec_ext(4), vec_axis_is_local(4)

 integer*4 ier

 mat_axis_is_local(1) = 1

 mat_axis_is_local(2) = 1

 mat_axis_is_local(3) = 0

 mat_axis_is_local(4) = 0

 mat_axis_is_local(5) = 0

 mat_ext(1) = p

 mat_ext(2) = q

 mat_ext(3) = k

 mat_ext(4) = m

 mat_ext(5) = n

 call s3l_declare(a, 5, mat_ext, S3L_float, mat_axis_is_local,

$    S3L_USE_MALLOC, ier)

 vec_axis_is_local(1) = 1

 vec_axis_is_local(2) = 1

 vec_axis_is_local(3) = 0

 vec_axis_is_local(4) = 0

 vec_ext(1) = q

 vec_ext(2) = k

 vec_ext(3) = m

 vec_ext(4) = n

 call s3l_declare(x, 4, vec_ext, S3L_float, vec_axis_is_local,

$    S3L_USE_MALLOC, ier)

 vec_ext(1) = p

 vec_ext(2) = k

 vec_ext(3) = m

 vec_ext(4) = n

 call s3l_declare(y, 4, vec_ext, S3L_float, vec_axis_is_local,

$    S3L_USE_MALLOC, ier)

The data axes are defined to be local to a process. Each array has three block-distributed instance axes. Note that the order of instance axes is the same in all three arrays.

Multiplication using these arrays is then performed by

call S3L_mat_vec_mult(y, a, x, 1, 1, 2, 1, ier)

The following is an analysis of the results of this multiple-instance matrix-vector operation. In this analysis, s0, s1, and s2 are used to denote the index along each of the three instance axes. For a given value of s0, the following operations will be done:

The product a(i, j, s0, s1, s2) * x(j, s0, s1, s2) will be calculated for all j. This is indicated by the values of the arguments x_vector_axis and col_axis, which are 1 and 2, respectively.

This product will be summed over i, the first index of a (row_axis = 1), and the result added to y(i, s0, s1, s2).

These two operations will be performed for all 1 <= s0 <= k, 1 <= s1 <= m, and
1 <= s2 <= n. In other words, the matrix-vector multiplication will be evaluated for all instances:

y(:, s0, s1, s2) = A(:, :, s0, s1, s2) * x(:, s0, s1, s2)

However, unlike the previous example, the data axes in this case are local. This means that the evaluation of each instance does not involve any interprocess communication. Each process independently works on its own set of instances, using a purely local matrix-vector multiplication algorithm. These local algorithms are usually faster than their global counterparts, since no communication between processes is involved.

Source code for these operations is in the file mat_vec_mult.f. This can be found in the Sun S3L examples directory:

/opt/SUNWhpc/examples/s3l/dense_matrix_ops-f.

Note - /opt/SUNWhpc is the default location for the examples directory. If you cannot find the directory, it may be that your site is not using the default path.

Example 2: Fast Fourier Transforms

When calling the detailed complex-to-complex FFT routine, S3L_fft_detailed, you can supply a multidimensional parallel array and specify whether you want to perform a forward transform, an inverse transform, or no transform along each axis. The axes that are transformed are the data axes and define the cell. The axes along which no transformation is performed are the instance axes.

Note - The simple FFT routine, S3L_fft, performs a transform along each axis of the supplied parallel array. Consequently, it does not support multiple instances.