Suntrademark S3L 4.0 Software Programming Guide Table of ContentsPrevious ChapterNext ChapterNoIndex


C H A P T E R  3
Sun S3L Arrays

This chapter discusses various issues related to parallel arrays in the Sun S3L context. This discussion is organized into the following sections:

Overview

Sun S3L distributes arrays on an axis-by-axis basis across multiple processes, enabling operations to be performed in parallel on different sections of the array. These distributed arrays are referred to in this manual as Sun S3L arrays. They may also be referred to as Sun S3L parallel arrays.

When a message-passing program passes an array to a Sun S3L routine, it can specify any of the following distribution methods for the array's axes:

Regardless of the distribution scheme specified by the calling program, Sun S3L will, if necessary, automatically distribute the axes internally in a manner that is most efficient for the routine being called. If Sun S3L changes the distribution method internally, it will restore the original distribution scheme on the resultant array before passing it back to the calling program.

Sun S3L Array Attributes

A principal attribute of Sun S3L arrays is rank--that is, the number of dimensions, or axes, the array has. For example, a Sun S3L array with three dimensions is called a rank-3 array. Sun S3L arrays can have up to 31 dimensions.

A Sun S3L array is also defined by its extents, which is its length along each dimension, and its type, which refers to the data type of its elements. The following data types are defined for Sun S3L arrays:

The C and Fortran equivalents of these array data types are described in Chapter 2.

Array Indexing

Sun S3L routines that access specific locations within arrays use either zero-based or one-based indexing:

Sun S3L Array Handles

Each Sun S3L array must be associated with a unique Sun S3L array handle. This is a set of internal data structures that contains a full description of the array--that is, all the information needed to define both the global and local characteristics of the array. The global definition includes such information as the array's rank and how it is distributed. The local information includes its extents and its location in the local process memory. No matter how an array has been distributed, the associated Sun S3L array handle ensures that its layout is understood by all MPI processes.

In C programs, Sun S3L array handles are declared as type S3L_array_t and in Fortran programs as type integer*8.

Creating Sun S3L Array Handles

TABLE 3-1 lists the routines that Sun S3L provides for creating Sun S3L array handles.

TABLE 3-1 Sun S3L Routines for Creating Array Handles

Routine

Notes

Comments 

S3L_declare

dense

Allocates memory for a dense parallel array and returns a Sun S3L array handle that describes the array. 

S3L_declare_detailed

dense 

 

Same as S3L_declare, but this routine gives the user control over more array mapping parameters. 

S3L_declare_sparse

sparse 

 

Allocates memory for a sparse parallel array and returns a Sun S3L array handle that describes the array. This routine is used to set up sparse Sun S3L arrays for various sparse matrix and sparse linear systems functions. 

S3L_read_sparse

sparse 

 

Sets up a sparse matrix and reads sparse matrix data from a file into it. The nonzero values are mapped into the matrix in terms of the sparse data structure stored in the file. 

S3L_rand_sparse

sparse 

 

Sets up a sparse matrix and populates it with random nonzero values in a sparsity pattern that is specified by arguments in the function argument list.


Detailed descriptions of S3L_declare and S3L_declare_detailed are provided in Creating and Destroying Array Handles for Dense Sun S3L Arrays.

S3L_declare_sparse, S3L_read_sparse, and S3L_rand_sparse are described more fully in Chapter 12.

There are three other Sun S3L routines that also create Sun S3L array handles, but they are meant for special-case situations. They are listed in TABLE 3-2.

TABLE 3-2 Routines for Creating Sun S3L Array Handles in Special Cases

Routine

Notes

Comments

S3L_convert_sparse

sparse

Converts a sparse array from one supported sparse format to another supported sparse format. There are four such supported sparse formats.

S3L_from_ScaLAPACK_desc

dense

Converts a ScaLAPACK array descriptor to a Sun S3L array handle.

S3L_DefineArray

dense

This routine is an earlier version of S3L_declare, but its user interface is less efficient. It is retained only for compatibility with the Sun HPC 2.0 release of Sun S3L.


These routines are all described in the Sun S3L Software Reference Manual.

Deallocating Sun S3L Array Handles

When a Sun S3L array is no longer needed, use S3L_free to deallocate a dense array and S3L_free_sparse to deallocate a sparse array. This makes the memory resources available for other uses.

MPI Processes and Sun S3L Process Grids

In a Sun MPI application, each process is identified by a unique rank. This is an integer in the range 0 to np-1, where np is the total number of MPI processes spawned by the application.


Note - This use of the term rank is unrelated to the rank of a Sun S3L array. Process ranks correspond to MPI ranks as used in interprocess communication. A Sun S3L array's rank refers to the number of dimensions the array has.


Sun S3L maps each Sun S3L array onto a logical arrangement of MPI processes, referred to as a process grid. A process grid will have the same number of dimensions as the Sun S3L array with which it is associated. The section of a Sun S3L array that is on a given process is called a subgrid.

Sun S3L controls the ordering of the processes within the n-dimensional process grid. FIGURE 3-1 through FIGURE 3-3 illustrate this. These examples show how Sun S3L might arrange eight processes in one- and two-dimensional process grids.

In FIGURE 3-1, the eight processes form a one-dimensional grid.

 FIGURE 3-1 Eight Processes Arranged as a 1x8 Process Grid

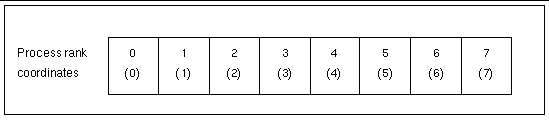
Graphic image depicting eight processes arranged as a 1x8 process grid.

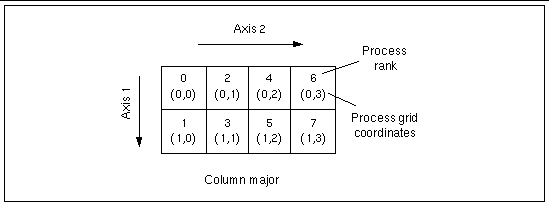
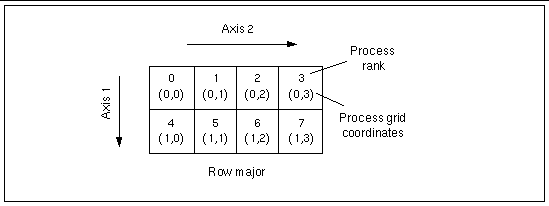
FIGURE 3-2 and FIGURE 3-3 show the eight processes organized into rectangular 2x4 process grids.

Note that, although both process grids have 2x4 extents, they differ in their majorness attribute. This attribute determines the order in which the processes are distributed onto a process grid's axes or local subgrid axes. The two possible modes are:

  • Column major - Processes are distributed along column axes first; that is, the process grid's row indices increase fastest.

  • Row major - Processes are distributed along row axes first; the process grid's column indices increase fastest.

In FIGURE 3-2, subgrid distribution follows a column-major order. In FIGURE 3-3, process grid distribution is in row-major order.

 FIGURE 3-2 Eight Processes Arranged as a 2x4 Process Grid: Column-Major Order

Graphic image depicting eight processes arranged as a 2x4 process grid: column-major order.

 FIGURE 3-3 Eight Processes Arranged as a 2x4 Process Grid: Row-Major Order

Graphic image depicting eight processes arranged as a 2x4 process grid: row-major order.

Note - In these examples, axis numbers are one-based (Fortran-style). They would be zero-based for the C-language interface. Process ranks and process grid coordinates are always zero-based.


Creating Process Grids

By default, Sun S3L will automatically assign a process grid of an appropriate shape and size whenever a Sun S3L array handle is created. In choosing a default process grid, Sun S3L always has the goal of producing as even a distribution of the Sun S3L array as possible.

However, the programmer has the option of defining a process grid explicitly by calling the function S3L_set_process_grid. This enables the programmer to specify:

  • The number of dimensions the process grid will have

  • The order in which the axes are created: column major or row major

  • The extent of each of the process grid's axes

  • The list of processes to be included in the process grid

Upon exit, S3L_set_process_grid returns a process grid handle.

A process grid can be defined over the full set of processes being used by an application or over any subset of those processes. This flexibility can be useful when circumstances call for setting up a process grid that does not include all available processes.

For example, if an application will be running in a two-node cluster where one node has 14 CPUs and the other has 10, better load balancing may be achieved by defining the process grid to have 10 processes in each node.

When the process grid is no longer needed, you can deallocate its process grid handle by calling S3L_free_process_grid.

Detailed descriptions of S3L_set_process_grid and S3L_free_process_grid are provided in Creating a Custom Process Grid.

Distributing Sun S3L Arrays

Sun S3L array axes are distributed either locally or in a block-cyclic pattern. When an axis is distributed locally, all indices along that axis are made local to a particular process.

An axis that is distributed block-cyclically is partitioned into blocks of some useful size and the blocks are distributed onto the processes in a round-robin fashion:

  • The first block goes to the first process, the second block to the second process, and so on. This continues until all processes have received an initial block.

  • After the last process in the sequence has received its first block, the next block is sent to the first process, the block after that to the second process, and so on. This cycle is repeated until all elements in the axis have been distributed.

The definition of a useful block size will vary, depending in large part on the kind of operation to be performed. See the discussion of Sun S3L array distribution in the Sun HPC ClusterTools Software Performance Guide for additional information about block-cyclic distribution and choosing block sizes.

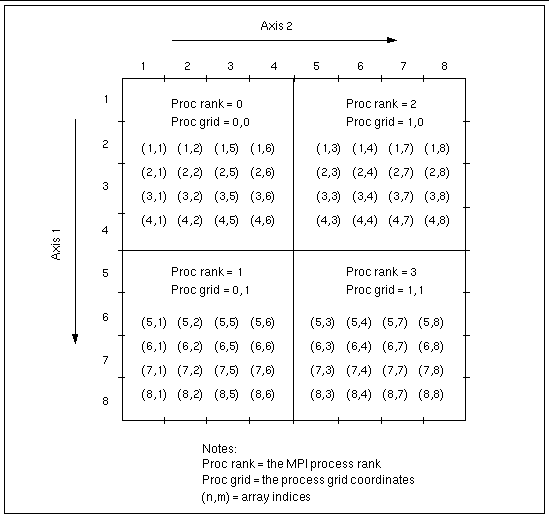
A special case of block-cyclic distribution is block distribution. This involves choosing a block size that is large enough to ensure that all blocks in the axis will be distributed on the first distribution cycle--that is, no process will receive more than one block. FIGURE 3-4 through FIGURE 3-6 illustrate block and block-cyclic distributions with a sample 8x8 array distributed onto a 2x2 process grid.

In FIGURE 3-4 and FIGURE 3-5, block size is set to 4 along both axes and the resulting blocks are distributed in pure block fashion. As a result, all the subgrid indices on any given process are contiguous along both axes.

The only difference between these two examples is that process grid ordering is column-major in FIGURE 3-4 and row-major in FIGURE 3-5.

 FIGURE 3-4 An 8x8 Sun S3L Array Distributed on a 2x2 Process Grid Using Pure Block Distribution: Column-Major Ordering of Processes

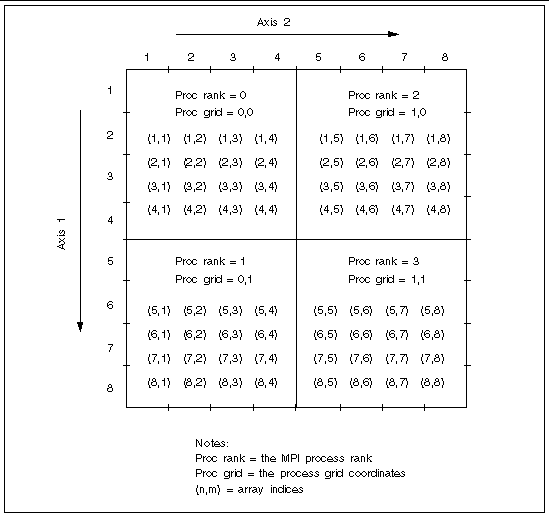
Graphic image depicting an 8x8 S3L array distributed on a 2x2 process grid (pure block distribution): column-major order.

 FIGURE 3-5 An 8x8 Sun S3L Array Distributed on a 2x2 Process Grid Using Pure Block Distribution: Row-Major Ordering of Processes

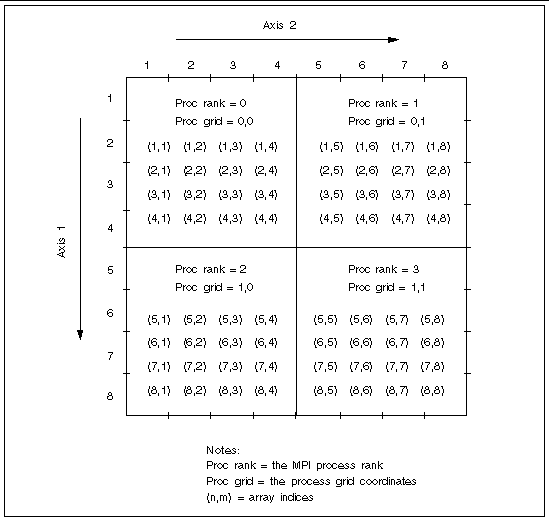
Graphic image depicting an 8x8 S3L array distributed on a 2x2 process grid (pure block distribution): row-major order.

FIGURE 3-6 shows block-cyclic distribution of the same array. In this example, the block size for the first axis is set to 4 and the block size for the second axis is set to 2.

 FIGURE 3-6 An 8x8 Sun S3L Array Distributed on a 2x2 Process Grid Using Block-Cyclic Distribution: Column-Major Ordering of Processes

Graphic image depicting an 8x8 S3L array distributed on a 2x2 process grid (block-cyclic distribution): column-major order.

When no part of a Sun S3L array is distributed--that is, when all axes are local--all elements of the array are on a single process. By default, this is the process with MPI rank 0. The programmer can request that an undistributed array be allocated to a particular process with the S3L_declare_detailed routine.

Although the elements of an undistributed array are defined only on a single process, the Sun S3L array handle enables all other processes to access the undistributed array.

Examining the Contents of Sun S3L Arrays

Printing Sun S3L Arrays

The Sun S3L utilities S3L_print_array and S3L_print_sub_array can be used to print the values of a distributed Sun S3L array to standard output.

S3L_print_array prints the whole array, while S3L_print_sub_array prints a section of the array that is defined by programmer-specified lower and upper bounds.

The values of array elements will be printed out in column-major order. This is referred to as Fortran ordering, where the leftmost axis index varies fastest.

Each element value is accompanied by the array indices for that value. This is illustrated by the following example.

a is a 4 x 5 x 2 Sun S3L array that has been initialized to random double-precision values with a call to S3L_rand_lcg. A call to S3L_print_array will produce the following output: 

    call s3l_print_array(a)

(1,1,1)    0.000525

(2,1,1)    0.795124

(3,1,1)    0.225717

(4,1,1)    0.371280

(1,2,1)    0.225035

(2,2,1)    0.878745

(3,2,1)    0.047473

(4,2,1)    0.180571

(1,3,1)    0.432766

...

For large Sun S3L arrays, it is often a good idea to print only a section of the array rather than the entire array. This not only reduces the time it takes to retrieve the data, but it can be difficult to locate useful information in displays of large amounts of data. Printing selected sections of a large array can make the task of finding data of interest much easier. This can be done using the function S3L_print_sub_array. The following example shows how to print only the first column of the array shown in the previous example: 

    integer*4 lb(3),ub(3),st(3)

 

c        specify the lower and upper bounds

c        along each axis. Elements whose coordinates

c        are greater or equal to lb(i) and less than or

c        equal to ub(i) (and with stride st(i)) are

c        printed to the output

    lb(1) = 1

    ub(1) = 4

    st(1) = 1

    lb(2) = 1

    ub(2) = 1

    st(2) = 1

    lb(3) = 1

    ub(3) = 1

    st(3) = 1

    call s3l_print_sub_array(a,lb,ub,st,ier)

The following output would be produced by this call: 

(1,1,1)    0.000525

(2,1,1)    0.795124

(3,1,1)    0.225717

(4,1,1)    0.371280

If a stride argument other than 1 is specified, only elements at the specified stride locations will be printed. For example, the following sets the stride for axis 1 to 2: 

st(1) = 2

which results in the following output: 

(1,1,1)    0.000525

(3,1,1)    0.225717

Visualizing Distributed Sun S3L Arrays With Prism

Sun S3L arrays can be visualized with Prism, the debugger that is part of the Sun HPC ClusterTools suite. Before Sun S3L arrays can be visualized, however, the programmer must instruct Prism that a variable of interest in an MPI code describes a Sun S3L array.

For example, if variable a has been declared in a Fortran program to be of type integer*8 and a corresponding Sun S3L array of type S3L_float has been allocated by a call to S3L_declare or S3L_declare_detailed, the programmer should enter the following at the Prism command prompt: 

type float a

Once this is done, Prism can print values of the distributed array: 

print a(1:2,4:6)

Or it can assign values to it: 

assign a(2,10) = 2.0

or visualize it: 

print a on dedicated



  Suntrademark S3L 4.0 Software Programming Guide 817-0086-10 Table of ContentsPrevious ChapterNext ChapterNoIndex


Copyright © 2003, Sun Microsystems, Inc. All rights reserved.